A Beginning Conception of Speed When Acceleration is Constant by Charles Hohensee, SDSU / UCSD

Introduction

What kind of conception should students have of constantly increasing speed?  This is a central research question that this study is attempting to address.  Beginning in the 8^th grade, students are being asked to solve Algebra and Physics problems involving constantly increasing speed.  However, this is a very complex concept.  Normally one thinks about a speed, (eg. 3 meters per second), as the motion required to go a certain distance (3 meters) in a certain interval of time (1 second).  But, when speed is always changing, a given speed defines the motion for only an instant of time.  Therefore, students need to find new ways to think about speed.

Of course, calculus was created to deal with these complex ideas.  The problem is that calculus will not be accessible to 8^th graders for at least several years.  The traditional response to this problem has been to teach 8^th graders the formulas by which they can solve problems involving increasing speed, with the assumption that they will not develop meaning for these formulas until they take calculus.  However, this perpetuates the student belief that mathematics and science is about memorization and not about sense-making.  It has been well-documented that students that memorize procedures for solving problems often stop trying to build understanding (Smith & Thompson, 2007).  Thus, it seems important that mathematics teachers find ways to help students develop more robust understandings of constantly increasing speed.

In the study reported here we investigated how nine 8^th graders, in an after school algebra enrichment program, were making sense of constantly increasing speed.  What proved to be informative were students’ interactions with their diagrams for a particular problem involving a falling ball.  Several issues emerged as being particularly difficult.  This helped us began to see the kind of conception of increasing speed that might be accessible to an 8^th grader.

Literature Review

In this section, I will present a review of literature pertaining to developing a beginning understanding of increasing speed.

Quantity:  During the planning for the after school program and during the subsequent analysis, substantial consideration was given to how students conceive of time, distance, speed and acceleration as quantities and how they distinguish between them.  Therefore, it became important to ground ourselves in the mathematics education literature about quantity.

Thompson (1994) describes quantities as consisting of three parts: “a quality of the object, an appropriate unit or dimension, and a process by which to assign a numerical value to the quality” (p. 184).  According to Lobato and Thanheiser (2002), a quantity is “an aspect of an object or situation that can be measured” (p. 162).  Olive and Çağlayan (2008) describe quantity as an ordered pair, consisting of a name and a measure.  Thompson and Olive and Çağlayan agree that quantities do not exist on their own but are conceptual entities that are constructed by a process of assimilations of experiences that involve quantitative reasoning.

Units:  The Oxford English Dictionary [Online] definition is “[a]ny determinate quantity, dimension, or magnitude adopted as a basis or standard of measurement for other quantities.”  Steffe (1991) describes unitizing as the mental operations involved in forming extensive quantities from gross quantities.  Therefore, attaching a label to a numerical value is not sufficient evidence that unitizing has occurred.  What comprises sufficient evidence of unitizing is, a) showing recognition of the unitized quantity and b) re-presenting the unitized quantity in “absence of the sensory-motor experiences” (p. 66).

Speed:  In mathematics education literature, the traditional approach has been to develop students’ conception of speed as a rate (Thompson & Thompson, 1994; 1996).  However, students often move through some intermediate conceptions of speed.  Piaget (1970; in Thompson, 1994) found that children’s conception of speed is distinct from the phenomenon of motion and that it is not until students develop proportional reasoning that they begin to see that speed is entailed by motion.  Thompson and Thompson (1994, 1996) found that students often think of speed as a speed-length, where the distance traveled in a unit of time is given more status than the time.  Lobato and Thanheiser (2002) found that in the context of a race, students “associated speed with time” (p. 170).  Intermediate conceptions of speed led Stroup (2002) to argue that “…[t]he constant speed context is too simple to, by itself, support students’ sense-making related to differentiating and then reintegrating their understandings of the relationships between how fast and how much quantities, like slope and intercept” (p. 182).

The after school program was based on using squares of area to represent distance traveled, with the horizontal dimension representing time and the vertical dimension representing speed.  Nichole Oresme (14^th century) is widely acknowledged to have been the first known person to represent distance, speed and time in this way (Gravemeijer & Doorman, 1999; Stroup, 2002).  Historically, ideas about constantly increasing speed began as approximations and developed into more formal mathematical ideas involving calculus.  This historical evidence is used to support the argument that the calculus curriculum should also begin with approximations and move to more formal concepts.

Acceleration:  There seems to be very little written about developing a conception of increasing speed in the mathematics education literature.  However, several articles from science education address the conception of acceleration.  Basson (2002) equates the complexity and importance of acceleration in physics curriculum with the complexity and importance of functions in mathematics curriculum.  Trowbridge and McDermott (1980, 1981) found that many university students enrolled in introductory physics had vague conceptions of the quantities involved in motion.  These vague conceptions were called “protoconcepts”.  For example, students often confused position and speed, as well as acceleration and speed, and also had difficulty seeing acceleration as a ratio.

Tool and Diagram Use:  Jones (2000) defines tools from a sociocultural perspective as “instruments of access to the knowledge, activity and practices of a community…(that) mediate the users action – they exist between the user and the world and transform the user’s activity upon the world” (p. 2).  Rasmussen and Marrongelle (2006) define a tool as “something the informed user explicitly recognizes as useful for achieving specific goals…includ[ing] graphs, diagrams, equations, verbal statements, gestures, thought experiments and so on” (p. 389).  Nemirovsky and Noble (1997) point out that a physical or conceptual object is not really used as a tool until some expertise or fluency with the object develops.

However, Nemirovsky, Teirney and Wright (1998) prefer to think of tool fluency as the development of a tool perspective, so as to avoid thinking about what happens as being a separate internal process.  They explain that “[a]dopting a tool perspective involves emulating the tool’s sensitivity to certain aspects of motion and not to others, ascertaining conditions under which the tool is useful, and recognizing patterns of significance in the tool’s products” (p. 125).  They also explain that in adopting a tool perspective, a student develops the ability to foreground features of the tool that are important and to background idiosyncratic features that are not important.

Representations, such as diagrams, can also function as tools (Noble, DiMattia, Nemirovsky, & Barros, 2006).  Diezmann and English (2001) explain that in order for students to use diagrams for problem solving, they need to be diagram literate, which means knowing why a diagram can be used for problem solving, knowing which diagram is appropriate for problem solving and knowing how to use the diagram to problem solve.  A lack of diagram literacy on a task could result in a diagram that is structurally inadequate or that represents surface features rather than structural features of the problem.

Methods

In this section, I will describe the participants, the instructional materials, the instructional sessions and the data analysis that comprised this study, which was designed and conducted within a larger 3-year National Science Foundation funded research project, led by Principal Investigator Joanne Lobato (SDSU).  The instructional sessions were conducted at a large urban middle school in a large southwestern U.S. city.  The school was ethnically diverse.

Participants:  The students that participated in the instructional sessions were recruited from four mathematics classes.  The students, nine 8^th graders, were chosen using a convenience sampling method, based on their willingness to participate and their availability.  Of the nine, seven were girls and two were boys.  Eight out of the nine students were Hispanic and one was African American.  It appeared that one of the girls was an English learner, but we were not given access to the students’ language designation.  Four of the nine were taking Algebra 1 at the time of the instructional sessions.  The other five were taking Pre-Algebra.

Instructional Materials:  The instructional materials focused on an exploration of a linearly increasing speed-time graph as part of a quadratic distance-time function.  This idea came from reading Rochelle, Kaput and Stroup (1998) who wrote, “middle school students can learn to predict position from a velocity graph by using two skills that they have already developed: counting and area multiplication.  The velocity graph…is drawn against a grid, which enables students to compute accumulated position by counting grid squares” (p. 16).  This idea held promise because it seemed to be accessible to 8^th graders.

The instructional sessions were roughly divided into two parts.  The first five sessions were about exploring a constant speed-time graph and representing a unit of distance with a unit of area.  The last ten sessions were about exploring a linearly increasing speed-time graph and representing the distance travelled with a triangle-shaped area under the graph.

Instructional Session:  The classes were conducted after school during the regular school year.  The author of this paper was the teacher for all fifteen 1-hour classes, which generally ran during consecutive school days.  Each meeting was held in one of the school’s math classrooms.  The students were placed in groups of three and each group was supplied a laptop computer.

The meeting structure alternated between whole class discussion and small group activities.  Students were encouraged to interact with each other in the small groups.  However, they tended to work more often individually than cooperatively.  This seemed to be a result of several factors: (a) the students were not that familiar with working cooperatively on mathematics; (b) the mathematics were different from what they learned in their normal math class; (c) the students felt somewhat self-conscious in a small class with a new teacher; and (d) the activities did not always necessitate cooperative learning.  Nevertheless, the students were generally very cooperative and tried to complete every task.

The laptops were loaded with Mathworlds software (Kaput, 1997).  I prepared “movies” of one or two characters, walking either at a constant speed or at constantly increasing speed.  Students were asked to explore, in small groups, the various relationships between distance, time and speed.  There were also whole class discussions that occurred after students had an opportunity to observe each other walk at constant speed and at constant acceleration.

Data Analysis:  The qualitative analysis of the interview data followed a Grounded Theory approach (Strauss & Corbin, 1990, 1994).  Several members of the research team, including myself, began by watching interview videos.  This led us to think that the way the diagrams were being constructed might warrant a closer look.  What emerged was that the productive interactions with diagrams, particularly by two students, and the unproductive interactions by several other students, pointed to a way of conceiving of speed in a constant acceleration context that might be both attainable and potentially useful.

Results and Discussion

In this section, I will present results from the post-interviews.  I will present findings in five areas: (1) types of diagrams that the students drew, (2) students’ methods for diagram construction, (3) students’ conceptions of elapsed distances, (4) students’ reasoning about their diagrams in relation to adopting a tool perspective, and (5) students’ connections between elapsed distance and speed.  After each set of results, I present a short discussion about implications for the research question 

Falling Ball Task:  Students were presented with a prompt about a falling ball (see Figure 1).  After students drew their pictures, the interviewer asked them questions about their drawing and the task.

Figure 1: Prompt for Falling Ball Task.

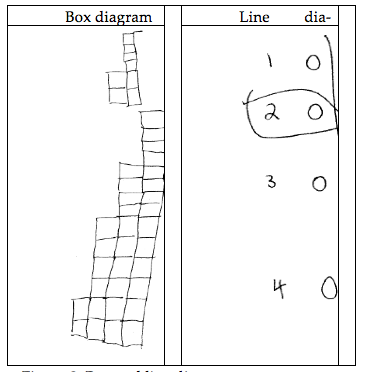
Types of Diagrams – Results:  Two types of diagrams were created by the students: box diagrams and line diagrams.  The box diagrams featured squares arranged in columns.  The leftmost column represented the first second of time and each subsequent column to the right represented the next second of time (see Figure 2).  Six of nine students made box diagrams.  Note that this definition of a column also implies that a column represents the distance covered in a second of time.  Only some of the students realized this.

The remaining three students did not draw box diagrams.  Instead they drew line diagrams, which featured a series of snap-shot pictures of a ball falling vertically.  Other contextual details of the diagram (boy dropping ball, edge of cliff, motion marks) were also present to varying degrees (see Figure 2).  All three students labeled each snapshot of the ball with a total distance and a total time.

Figure 2. Box and line diagrams.

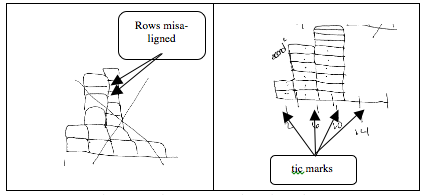
Method for Box Diagram Construction – Results:  There were two distinct methods that students used to construct the box diagrams.  The first method emphasized the columns.  The first step of this method was to outline a column.  The second step was to extend rows of the previous column to segment the new column.  The second method was to draw each square individually, putting one box on top of the next to build each column.  Three students used this method for some or all of their diagram construction (see Figure 3).

Method for Box Diagram Construction – Discussion:  As stated above, the first method seemed to emphasize columns which may have led to seeing the columns as composite units.  This is because drawing the column first likely created moments of focused attention (Steffe, 1991) directed at the column.  In contrast, the second method seemed to emphasize the individual boxes.  Because it did not have the same level of focused attention on an entire column, the second method likely led to seeing individual boxes as unitary items.

Conceptions of the Differences of Distances – Results:  The mathematical differences that emerged in this task were the differences between the total distance covered at one time compared to the total distance covered the second before.  These differences will be referred to as elapsed distances.  We found evidence of some students conceiving of the elapsed distances numerically and some conceiving of them quantitatively (Thompson, 1993).

Dina and Evelyn provided evidence of conceiving of elapsed distances as quantitative differences.  For example, Dina was able to find and report elapsed distances from total distance-time data.  She also showed she was able to compare elapsed distances when she said, “[t]he last second, because, you can see the difference from the first and the fourth.  It’s a twelve difference, a difference of twelve.”  She also consistently reported the elapsed distances as speeds.

Two other students showed evidence that they saw the elapsed distances as numerical differences.  These students, Mariette and Arianna, determined elapsed distances but assigned no meaning or significance to the values.  When Mariette explained her diagram, she said, “then at the 2^nd second, it went to eight meters, so if you take…you put six more meters and two seconds, so that’s eight altogether.  Then it went eighteen, so you add ten more.  And then after thirty-two and you add however many more.”  However, she never referred to these distances at any other time in the interview, even when asked about speed.  Similarly, Arianna referred to the distances in her box diagram at the beginning of the task, and not during the rest of her interview.

Alice and Conner showed some evidence of conceiving of elapsed distance as quantitative differences, but not at the same consistent level as Evelyn and Dina.  Alice found the elapsed distances in her drawing, but did not report them as speeds until near the end of the task, after working with a graph.  A group of three students, Karmen, Ernie and Rita, did not show any significant evidence of considering elapsed distances.

Conceptions of the Differences of Distances – Discussion:  The comparison of pairs, Evelyn and Dina with Mariette and Arianna, revealed a sharp contrast with respect to diagrams and conceptions of elapsed distance.  On the one hand, Evelyn and Dina constructed their diagrams using a method that seemed to promote columns as a prominent feature and talked about elapsed distances as quantities.  On the other hand, Mariette and Arianna constructed their diagrams using a method that seemed to promote individual boxes as a prominent feature and talked about elapsed distances as numerical differences.  This contrast suggests both that 1) conceiving of elapsed distance as a quantitative difference may be part of what motivates outlining a column first, as if to distinguish it from the rest of the diagram and that 2) part of what motivates drawing the boxes individually may be seeing the elapsed distances predominantly as numerical differences.

Adopting a tool perspective – Results:  Diagrams function as tools when they help students gain access to knowledge or when they are used to achieve specific goals.  The students in this study seemed to be using diagrams to access knowledge to varying degrees of effectiveness.  Three characteristics of adopting a tool perspective are outlined by Nemirovsky et al. (1998): (a) emulating the tool’s sensitivity to certain aspects of motion; (b) recognizing patterns of significance in the tool’s products; and (c) foregrounding important features of the tool, while backgrounding superficial or unimportant features.

All six students who drew box drawings found elapsed distances, even though some conceived of them as numerical values only.  In contrast, none of the students that drew line diagrams found elapsed distances.  Thus, the students who drew box diagrams appeared to be showing greater sensitivity to the motion of the ball.

The students that drew box diagrams showed evidence of the second characteristic of adopting a tool perspective: they recognized patterns in their diagrams.  The pattern that they recognized was the value of the acceleration.  For example, Arianna said, “The 4 right here, it keeps going up by 4” [points]. By recognizing the value of the acceleration, students showed that they were recognizing patterns that were produced by the box diagram tool.  All six students who drew box diagrams recognized this pattern, even though not all used the same units.  In contrast, none of the students that drew line diagrams recognized the value of the acceleration.

An important feature of the box diagram is that a high level of spatial structuring can be used to draw the diagram.  As stated earlier, Battista et al. (1998) suggest that a high level of spatial structuring of rectangular arrays means row and column alignment.  Consistent use of hash marks is also a sign of spatial structuring.  Evelyn and Dina showed more evidence of recognizing this important feature of their diagrams, because they showed the most consistent row and column alignment.  In contrast, Alice’s first diagram contained rows that did not align (see Figure 3).

Rita showed a lack of awareness by assigning undue prominence to a superficial feature of her diagram.  For example, when asked if there was something in her drawing that indicated where the ball was going the fastest she said, “This thingee falling off the ball…yes, it’s so fast”.  Here she relies on the motion marks coming off the lowest ball as the indication that it is going the fastest, instead of relying on the data.

Adopting a tool perspective – Discussion:  It appears that the students who drew box diagrams were adopting a tool perspective to a greater degree than the students who drew line diagrams.  Presumably, this is because of the many opportunities the students had during the instructional session to become fluent users of the box diagram.

The students that drew box diagrams also seemed to vary in the degree to which they adopted a tool perspective.  In fact, how the students varied on adopting a tool perspective accorded with how they varied regarding their diagram construction method and their conception of differences.  Evelyn and Dina, who were the most consistent in outlining the columns of their diagrams first and in showing that they conceived of elapsed distances as quantitative differences, also seemed to show the highest degree of adopting a tool perspective.  Mariette and Arianna, who drew their diagrams with individual boxes and who showed evidence of conceiving of elapsed distances as numerical differences, appeared to show the lowest degree of adopting a tool perspective of the students that drew box diagrams.  It should be noted that the evidence presented above does not imply that line diagrams could not be effectively used as tools.

Synthesis of Results

The central question that this study is trying to address is what kind of conception should students have of constantly increasing speed?  As previously stated, conceiving of constantly changing speed as a ratio may be initially confusing for 8^th grade students because the ratio keeps changing and because students may not yet even have a clear understanding of constant speed.

In this section, I shall cohere the ideas from the short discussions that followed each set of results.  I shall outline how the various results presented above point to a conception of constantly changing speed that was attainable for two of the participants and that, I feel, may be useful as a beginning conception.

Conception of constantly changing speed:  It became apparent during the analysis of the results that Evelyn and Dina were providing more productive responses than the other students.  During their interaction with their diagrams, Evelyn and Dina showed a similarity that, I believe, served as the linchpin for their understanding of the falling ball task: they both showed evidence that they were conceiving of elapsed distances as quantitative differences.

There are three reasons why I believe this to be at the center of their understanding.  The first reason is that conceiving of elapsed distances as quantitative differences could have been what was motivating Evelyn and Dina to outline columns in their box diagram first.  The second reason is that conceiving of elapsed distances as quantities may have been what fostered a more developed tool perspective.  Even within the group of students who drew box diagrams, Evelyn and Dina were more fluent tool users.  The third reason is that it may have enabled Evelyn and Dina to make the connection between distances traveled in one second and speeds, something the other students were not able to do.  Perhaps not conceiving of elapsed distance as a quantity was what prevented these other students from connecting it to speed and/or perhaps conceiving of elapsed distance as a quantity is what enabled Evelyn and Dina to make the connection between distance traveled in one second and speed.

Based on these results and inferences about Evelyn and Dina, I would like to propose that a useful beginning conception of speed, when the speed is constantly increasing (or decreasing), that seems to be accessible to 8^th graders, would be speed as elapsed distance in a given time.  This conception of speed postpones the need to find instantaneous speeds and allows students to reflect on imaginable quantities rather than infinitesimal ones.  As stated earlier, Piaget (1970; in Thompson, 1994) found that an intermediate conception of speed existed before proportional reasoning developed.  Perhaps, an intermediate conception of increasing (or decreasing) speed could also exist prior to the student developing the necessary understanding of calculus with respect to constantly changing speed.  As the data has seemingly shown, this conception of speed appears to provide a core of understanding that allows students to reason quantitatively about speeding up.  This conception of speed also fits with Gravemeijer and Doorman’s (1999) suggestion to begin with approximations and move toward more formalized mathematics.

Of course, elapsed distance in a given time is nothing more (or less) than average speed.  However, what I am trying to emphasize here is that students need to come to see the part of average speed that is the elapsed distance as a quantitative difference.  It seems that calling speed an average, or thinking about it as an average, may complicate the quantitative aspect of the elapsed distance for students who are just beginning to think about constantly increasing speed.

Some may think that speed as elapsed distance in a given time may create a similar misconception to that which Thompson (1994) labeled “speed-length”.  Some of the students in this study were even referring to speed with meters as units.  One might ask, “How could a productive conception of speed have such a strong emphasis on distance?”  I would agree that deemphasizing time would be unproductive.  That is why the composition of the column as a composite unit became such an important visual feature of the box diagrams.  It gave salience to time (even when the students referred to the units of speed as “meters”).  Therefore, if one were to use this proposed conception of speed with another approach to explore increasing speed, I would recommend that some effective method be found for ensuring that time was receiving equal emphasis.

Summary

The goal was to study students’ initial conceptions of constant acceleration. This seems to be under-addressed in both the mathematics and science education literature, in spite of acceleration being a prominent topic in high school Physics and Algebra.  However, it became clear in the early stages of analysis that this was a bigger task than anticipated.  What became the more immediate issue was that pertaining to what conception of increasing speed students should have if they were not yet ready for conceiving instantaneous changes in speed.

The diagrams that students drew for the falling ball task became a primary focus for analysis because there were distinctly different ways that students were interacting with their diagrams.  These different ways of interacting (constructing, talking, noticing, etc.) reflected different conceptions of elapsed distance.  It became apparent that the students who were conceiving of elapsed distances as quantitative differences were providing consistent evidence of a more sophisticated understanding of the data than the other students.  The conclusion from these results is that conceiving speed as elapsed distance in a given amount of time may be a productive way to conceive of speed in contexts where an object has constant acceleration, particularly if students have only recently begun to learn about constant acceleration and quadratic functions.

REFERENCES

Basson, I. (2002). Physics and mathematics as interrelated fields of thought development using acceleration as an example. International journal of mathematics education in science and technology, 33(5), 679-690.

Battista, M. T., Clements, D. H., Arnoff, J., Battista, K., and Van Auken Borrow, C. (1998). Students’ spatial structuring of 2D arrays of squares. Journal for Research in Mathematics Education, 29(5), 503-532.

Diezmann, C. M., & English, L. D. (2001). Promoting the use of diagrams as tools for thinking. In A. A. Cuoco and F. R. Curcio (Eds.), The Roles of Representation in School Mathematics. Reston, VA: National Council for Teachers of Mathematics.

Gravemeijer, K. & Doorman, M. (1999). Context problems in realistic mathematics education: A calculus course as an example. Educational Studies in Mathematics, 39, 111-129.

Jones, K. (2000), The Mediation of Mathematical Learning though the use of Pedagogical Tools: a sociocultural analysis. Invited paper presented at the conference on Social Constructivism, Socioculturalism, and Social Practice Theory: relevance and rationalisations in mathematics education, Norway, March 2000.

Kaput, J. (1997). SimCalc Mathworlds. North Dartmouth, MA: SimCalc Project.

Lobato, J., & Thanheiser, E. (2002). Developing understanding of ratio-as-measure as a foundation for slope. In B. Litwiller & G. Bright (Eds.), Making sense of fractions, ratios, and proportions, (pp.162-175). Reston, VA: NCTM.

Rasmussen, C., & Marrongelle, K. (2006). Pedagogical content tools: Integrating student reasoning and mathematics in instruction. Journal for Research in Mathematics Education, 37(5), 388-420.

Meira, L. (1998). Making sense of instructional devices: The emergence of transparency in mathematical activity. Journal for Research in Mathematics Education, 29(2), 121-142.

Nemirovsky, R., & Noble, T. (1997). On mathematical visualization and the place that we live. Educational Studies in Mathematics, 33, 99-131.

Nemirovsky, R., Teirney, C., & Wright, T (1998). Body motion and graphing. Cognition and Instruction 16(2), 119-172.

Noble, T., DiMattia, C., Nemirovsky, R., & Barros, A. (2006).  Making a circle: Tool use and the spaces where we live.  Cognition and Instruction, 24(4), 387-437.

Olive, J. & Çağlayan, G. (2008). Learner’s difficulties with quantitative units in algebraic word problems and the teacher’s interpretation of those difficulties. International Journal fo Science and Mathematics Education 6: 269-292.

Oxford English Dictionary [Online]. Available: http://www.oed.com (Accessed 23 September 2008).

Roschelle, J., Kaput, J., & Stroup, W. (1998). SimCalc: Accelerating students’ engagement with the mathematics of change. In M. Jacobson, & Kozma, R. (Eds.), Educational Technology and Mathematics and Science for the 21st Century (pp. 47-75). Hillsdale, NJ: Lawrence Erlbaum.

Smith, J., & Thompson, P. W. (2007). Quantitative reasoning and the development of algebraic reasoning. In J. Kaput, D. Carraher, & M. Blanton (Eds.), Algebra in the early grades (pp. 95-132). New York: Erlbaum.

Steffe, L. P. (1991). Operations that generate quantity. Learning and Individual Differences, 3(1), 61-82.

Strauss, A., & Corbin, J. (1990). Basics of qualitative research: Grounded theory procedures and techniques. Newbury Park, Calif.: Sage Publications.

Strauss, A., & Corbin, J. (1994). Grounded theory methodology: An overview. In N. K. Denzin, and Y. S. Lincoln (Eds), Handbook of Qualitative Research, Thousand Oaks: Sage Publications, pp.273-285.

Stroup, W. M., (2002). Understanding quantitative calculus: A structural synthesis of learning research. International Journal of Computers for Mathematical Learning, 7, 167-215.

Thompson, P. W., & Thompson, A. G., (1994). Talking about rates conceptually, Part 1: A teacher’s struggle. Journal for Research in Mathematics Education, 25(3), 279-303.

Thompson, A. G., & Thompson, P. W., (1996). Talking about rates conceptually, Part II: Mathematical knowledge for teaching. Journal for Research in Mathematics Education, 27(1), 2-24.

Thompson, P. (1994). The development of the concept of speed and its relationship to concepts of rate.  In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 179-234). Albany, NY: SUNY Press.

Thompson, P. W. (1993). Quantitative reasoning, complexity, and additive structures. Educational Studies in Mathematics, 25(3), 165-208.

Trowbridge, D. E., & McDermott, L. C. (1980). Investigation of student understanding of the concept of velocity in one dimension.  American Journal of Physics 48(2), 1020-1028.

Trowbridge, D. E., & McDermott, L. C. (1981). Investigation of student understanding of the concept of acceleration in one dimension.  American Journal of Physics 49(3), 242-253.